Bài giảng Đại số và Giải tích Lớp 11 - Tiết 1: Hàm số lượng giác

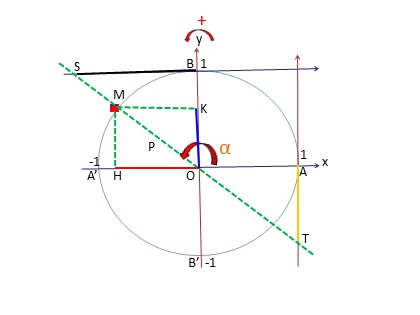
ủa hàm số y = sinx là R. 
Qui tắc tương ứng mỗi x R với số thực sinx 
x 
y 
sinx 
 sin : R R 
 x l y = sinx 
1)HÀM SỐ COSIN VÀ HÀM SỐ SIN : 
b)y = cos x : 
được gọi là hàm số cos , kí hiệu là y = cosx 
Tập xác định của hàm số y = cosx là R. 
Qui tắc tương ứng mỗi x R với số thực cosx 
 cos : R R 
 x l y = cosx 
x 
y 
cosx 
y 
x 
0 
cosx 
M 
Ví dụ : Tìm tập xác của mỗi hàm số sau : 
Trả lời : 
a)Do nên tập xác định của hàm số là D = R 
b) Để hs xác định thì sinx 0, nên tập xác định của hàm số là D = R\ { k ; k Z } 
c) Do 1- sinx 0 và 1+cosx 0, nên hs xác định thì 
1+cosx > 0, nên tập xác định của hàm số là 
D = R \ {( 2k+1) ; k Z } 
2)HÀM SỐ TANG VÀ HÀM SỐ COTANG : 
a) y = tanx : 
Tập xác định : D = R\ { /2 + k ; k Z } 
b)y = cotx : 
Tập xác định : D = R\ { k ; k Z } 
Hàm số tang là hàm số được xác định bởi công thức : 
Hàm số côtang là hàm số được xác định bởi công thức : 
x 
O 
B’ 
A 
B 
A’ 
y 
M 
x 
-x 
M’ 
Hãy so sánh các giá trị của sinx và sin(-x), 
cosx và cos(-x ) 
Trả lời : 
Sinx = - sin(-x) 
Cosx = cos(-x ) 
Nhận xét : 
Hàm số y= sinx là hs lẻ , 
hàm số y= cosx là hs chẵn, 
suy các hs y= tanx 
và y = cotx đều là hs lẻ . 
II- TÍNH TUẦN HOÀN CỦA HSLG: 
Ta nói chu kì của các hàm số : y = sinx là 2 
Tìm những số T sao cho f(x+T )= f(x ) với mọi x thuộc tập xác định của hàm số sau : 
a) f(x )= Sinx 
Trả lời : 
Sin(x + 2 )= sinx 
Sin(x - 2 )= sinx 
Sin(x + 4 )= sinx 
Tương tự chu kì của các hàm số : y = Cosx là 2 
tan(x + )= tanx 
tan(x - )= tanx 
tan(x + 2 )= tanx 
Ta nói chu kì của các hàm số : y = tanx là 
Tương tự chu kì của các hàm số : y = cotx là 
b) f(x ) = tanx 
1) Hàm số y = sinx : 
III- SỰ BIẾN THIÊN CỦA HÀM SỐ LƯỢNG GIÁC: 
Sự biến thiên của đồ thị y = sinx 
 trên đoạn [0; ] : 
x 1 ,x 2 (0; /2); x 1 <x 2 ta có :sinx 1 <sinx 2 
x 1 ,x 2 ( / 2 ; ); x 1 sinx 2 
Vậy , hàm số y = sinx : 
+ đồng biến trên khoảng ( 0 ; / 2 ). 
+ nghịch biến trên khoảng ( / 2 ; ). 
y 
y 
0 
0 
x 
x 
x 
 0 / 2 
y = sinx 
 1 
0 0 
 / 2 
1 
1) Hàm số y = sinx : 
y 
x 
0 
- 
- / 2 
 / 2 
1 
-1 
Trên đoạn [ - ; ], đ ồ thị đi qua các điểm : 
(0;0); ( /2;1); (- /2;-1); (- ;0);( ;0) . 
y 
x 
0 
Tập xác định D = R 
Hàm số lẻ 
Hàm số tuần hoàn , chu kì T = 2 
Tập giá trị : đoạn [ - 1; 1] 
- 
- / 2 
 / 2 
1 
-1 
2) Hàm số y = cosx : 
Tập xác định D = R 
Hàm số chẵn 
Tuần hoàn , chu kì T = 2 
Tập giá trị : đoạn [ - 1; 1] 
Lưu ý : sin (x+ /2 ) = cosx 
Từ đó ta có đồ thị hàm số cosx 
như sau : 
y 
x 
0 
- 
3) Hàm số y = tanx : 
Tập xác định : D = R \ { /2 +k ; k Z } 
Hàm số lẻ 
Tuần hoàn , chu kì T = 
Tập giá trị : R 
Tăng trên các khoảng : 
 (- / 2 + k ; / 2 + k ) 
x 
4) Hàm số y = cotx : 
Tập xác định : D = R \ { k ; k Z } 
Hàm số lẻ 
Tuần hoàn , chu kì T = 
Tập giá trị : R 
x 
CỦNG CỐ BÀI 
1) Khái niệm các hàm số lượng giác 
2) Nắm các tính chất của 4 HSLG : chẵn , lẻ ; tuần hoàn ; đơn điệu . 
3) Nhận dạng đồ thị của từng HSLG . 
 Ví dụ 1 : Tập xác định của hàm số : 
R	 B. R\{ /4+k ,k Z} 
C. [ -1;1]	 D.Một đáp số khác 
B 
CỦNG CỐ BÀI 
1) Khái niệm các hàm số lượng giác 
2) Nắm các tính chất của 4 HSLG : chẵn , lẻ ; tuần hoàn ; đơn điệu . 
3) Nhận dạng đồ thị của từng HSLG . 
 Ví dụ2 : Tập giá trị của hàm số 
y = 5sin(3x + 2) – 2 laø : 
[ - 1; 1]	B.( -7;7) 
C. [ -7;-2]	D.[- 7; 3] 
D 
BÀI TẬP VỀ NHÀ 
1 ĐẾN 8 (TRANG 17, 18 sgk ) 
Chúc các em học tốt !